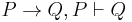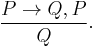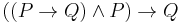Modus ponens
| Rules of inference |
|---|
| Propositional calculus |
| Modus ponens Modus tollens Modus ponendo tollens Conjunction introduction Simplification Disjunction introduction Disjunction elimination Disjunctive syllogism Hypothetical syllogism Constructive dilemma Destructive dilemma Biconditional introduction Biconditional elimination |
| Predicate calculus |
| Universal generalization Universal instantiation Existential generalization Existential instantiation |
In classical logic, modus ponendo ponens (Latin for "the way that affirms by affirming";[1] often abbreviated to MP or modus ponens) or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments. Both have apparently similar but invalid forms such as affirming the consequent or denying the antecedent and proof by contradiction or proof by contrapositive or evidence of absence.
Modus ponens is a very common rule of inference, and takes the following form:
- If P, then Q.
- P.
- Therefore, Q.[2]
Contents |
Formal notation
The modus ponens rule may be written in sequent notation:
or in rule form:
or as a tautology (plain propositional calculus sentence):
Explanation
The argument form has two premises. The first premise is the "if–then" or conditional claim, namely that P implies Q. The second premise is that P, the antecedent of the conditional claim, is true. From these two premises it can be logically concluded that Q, the consequent of the conditional claim, must be true as well. In artificial intelligence, modus ponens is often called forward chaining.
An example of an argument that fits the form modus ponens:
- If today is Tuesday, then John will go to work.
- Today is Tuesday.
- Therefore, John will go to work.
This argument is valid, but this has no bearing on whether any of the statements in the argument are true; for modus ponens to be a sound argument, the premises must be true for any true instances of the conclusion. An argument can be valid but nonetheless unsound if one or more premises are false; if an argument is valid and all the premises are true, then the argument is sound. For example, John might be going to work on Wednesday. In this case, the reasoning for John's going to work (because it is Wednesday) is unsound. The argument is not only sound on Tuesdays (when John goes to work), but valid on every day of the week. A propositional argument using modus ponens is said to be deductive.
In single-conclusion sequent calculi, modus ponens is the Cut rule. The cut-elimination theorem for a calculus says that every proof involving Cut can be transformed (generally, by a constructive method) into a proof without Cut, and hence that Cut is admissible.
The Curry-Howard correspondence between proofs and programs relates modus ponens to function application: if f is a function of type P → Q and x is of type P, then f x is of type Q.
Justification via truth table
The validity of modus ponens in classical two-valued logic can be clearly demonstrated by use of a truth table.
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
In instances of modus ponens we assume as premises that p → q is true and p is true. Only one line of the truth table—the first—satisfies these two conditions (p and p → q). On this line, q is also true. Therefore, whenever p → q is true and p is true, q must also be true.
See also
- Hypothetical syllogism
- Modus tollens
- Modus tollendo ponens
- Affirming the consequent
- Denying the antecedent
- Disjunctive syllogism
- Inference rule
- What the Tortoise Said to Achilles
References
- ^ Stone, Jon R. (1996). Latin for the Illiterati: Exorcizing the Ghosts of a Dead Language. London, UK: Routledge: 60..
- ^ Jago, Mark (2007). Formal Logic. Humanities-Ebooks LLP. ISBN 978-1-84760-041-7.
External links
- Modus ponens at Wolfram MathWorld